3-SAT Solver using CDCL

In Year 4, Sem 2, I took CS4244: Knowledge Based Systems at NUS, taught by Prof. Kuldeep Meel and Dr. Henry Chia.

This was one of the most insightful modules I took in NUS. It was different from any CS mod I’d taken before; there were no homework assignments or tests - we had 3 final projects, which were due at the end of the semester, and all of our tutorials and lectures were discussions rather than the profs using lecture notes to teach us something.

• In the first project, we had to research the CDCL algorithm and different heuristics for solving the 3-SAT problem (elaborated below). This was a team project.
• A second project involved using CLIPS, a logic-based language similar to Prolog and Lisp, to solve cryptarithmetic problems. This was an individual project.

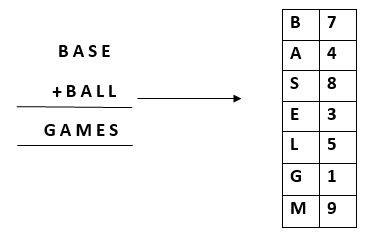
My CLIPS code is here.

3-SAT

In logic and computer science, the Boolean satisfiability problem determines if there are variables that satisfy a given Boolean formula. 3-SAT is an NP complete problem. E.g. (𝑥1 ∨ 𝑥2 ∨ 𝑥3) ∧ (𝑥4 ∨ 𝑥5∨ 𝑥6) if there are any values for x in [true, false] that satisfy (SAT) the entire clause. If not, the result is evaluated to be UNSAT.

There are many different algorithms which attempt to find whether a solution is SAT or UNSAT - one algorithm is called Conflict Driven Clause Learning, or CDCL, which my partner and I implemented in Python. SAT solving is at the core of computer science, and it is THE canonical NP Complete problem. Over the course of our research, we were amazed to find so many sources (and competitions!) dedicated to SAT Solvers, but in hindsight we realize we should have not been too surprised; SAT Solving can used in so many real world problems, e.g. scheduling, economics, etc.

Methods

After a lot of literature review, we decided on these methods to use:

• Unit Propagation
• Pick Branching
  • Variable State Independent Decaying Sum
  • Dynamic Largest Individual Sum
• Conflict Analysis and Backtracking
  • Constructed the implication graph
  • Identified the Unique Implication Point
• Resolution

Results

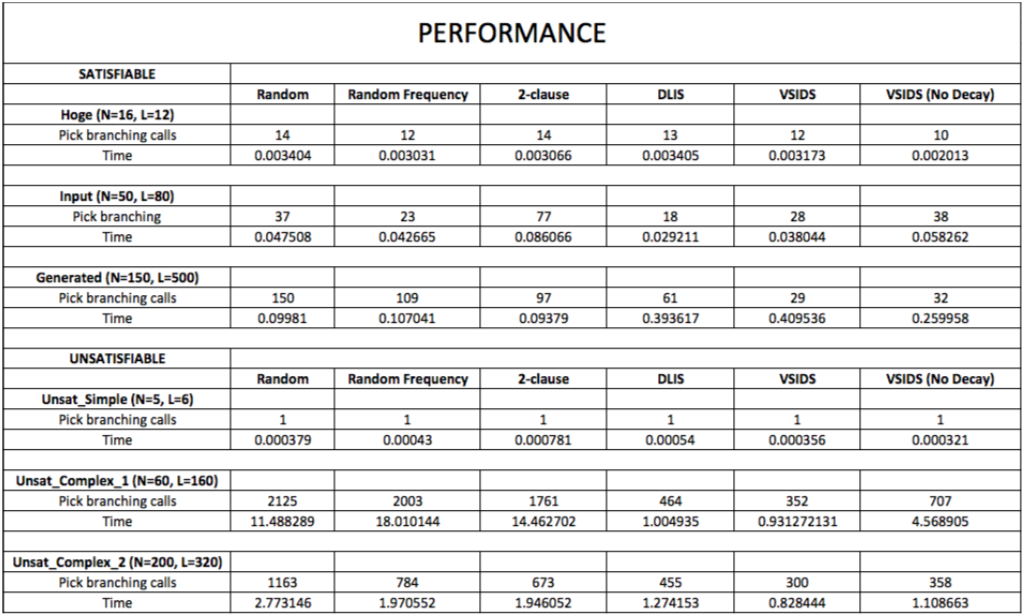
VSIDS was clearly the winner.

For our complete report, you can reach out to me via email.

Reflections

This project taught me a new way of learning; one where we weren’t spoon-fed and were able to make our own choices, without the threat of a deadline looming over our heads, for which I was grateful.

I believe this is how graduate school also works; if yes, then this was a good insight into the world of academia and independent thinking. And although I had to spend a lot of time self-learning, it was an immensely rewarding experience as I was quite satisfied with the work I did for this module, and I wish there were more modules like this at NUS - those which required thinking rather than competing with your cohort-mates.